Тройной интеграл.
1º. Мера Жордана в пространстве  .
.
Рассмотрим разбиение пространства на кубы 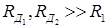 ранга
ранга 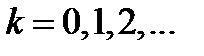 с помощью плоскостей
с помощью плоскостей 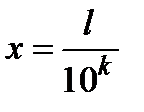 ,
, 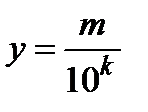 ,
, 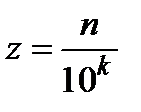 ,
, 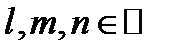 . Обозначим
. Обозначим 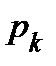 количество кубов
количество кубов 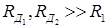 ранга, содержащихся во множестве
ранга, содержащихся во множестве 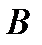 и
и 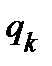 − количество кубов
− количество кубов 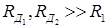 ранга, пересекающихся с множеством
ранга, пересекающихся с множеством 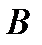 . Пусть ещё
. Пусть ещё 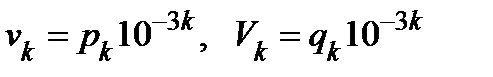 .
.
Определение. ВнутреннеймеройЖордана множества 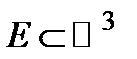 называется величина
называется величина 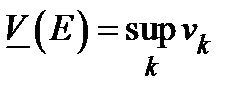 . Внешней мерой Жордана множества
. Внешней мерой Жордана множества 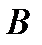 называется величина
называется величина 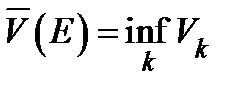 . Множество
. Множество 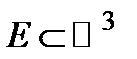 называется измеримым по Жордану или кубируемым, если
называется измеримым по Жордану или кубируемым, если 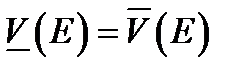 . Их общее значение
. Их общее значение 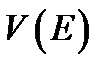 называется просто мерой этого множества или его объёмом.
называется просто мерой этого множества или его объёмом.
2º. Определение тройного интеграла.Пусть 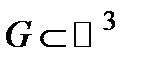 − кубируемое, ограниченное множество и
− кубируемое, ограниченное множество и 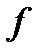 − функция, определенная на этом множестве. Рассмотрим разбиение
− функция, определенная на этом множестве. Рассмотрим разбиение 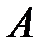 на неперекрывающиеся кубируемые подмножества
на неперекрывающиеся кубируемые подмножества 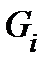 и выберем точки
и выберем точки 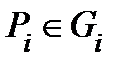 . Обозначим
. Обозначим 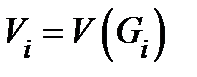 − объём множества
− объём множества 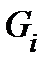 и
и 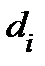 диаметр этого множества. Назовем мелкостью разбиения
диаметр этого множества. Назовем мелкостью разбиения 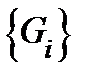 величину
величину 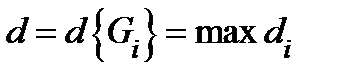 . Образуем интегральную сумму Римана
. Образуем интегральную сумму Римана 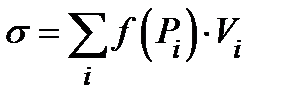 .
.
Определение.Если существует предел 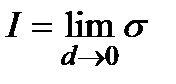 , то функция
, то функция 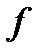 называется интегрируемой по Риману на множестве
называется интегрируемой по Риману на множестве 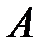 , в записи −
, в записи − 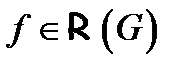 , а сам предел называется тройным интегралом и обозначается
, а сам предел называется тройным интегралом и обозначается 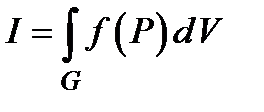 или
или 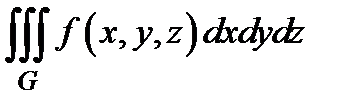 .
.
Точно так же, как в одномерном и двумерном случаях, формулируются и доказываются критерий интегрируемости, теорема о существования тройного интеграла от непрерывной функции и основные свойства интеграла. Отметим только, что средним интегральным в трёхмерном случае называют величину
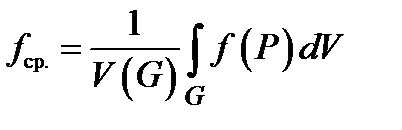 .
.
Замечание.По той же схеме определяется мера Жордана и интеграл в пространстве  при любом натуральном
при любом натуральном 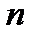 .
.
3º. Сведение кратных интегралов к повторным интегралам.
Пусть 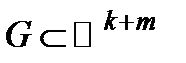 ,
, 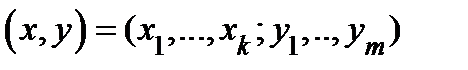 ;
; 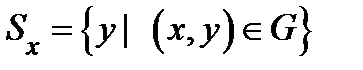 − сечение множества
− сечение множества 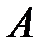 гиперплоскостью
гиперплоскостью  и пусть
и пусть 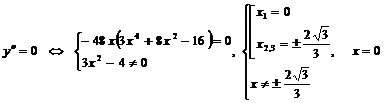 − проекция
− проекция 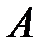 на подпространство
на подпространство 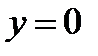 (т.е. на подпространство первых координат).
(т.е. на подпространство первых координат).
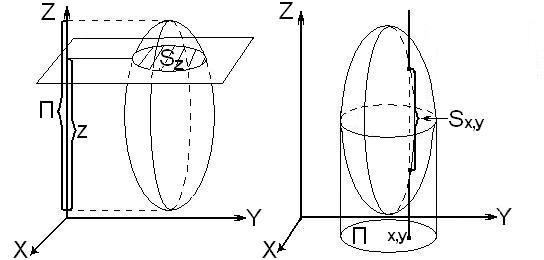
Теорема.Пусть существует интеграл 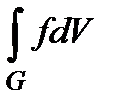 и пусть при любом значении
и пусть при любом значении 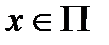 существует интеграл по сечению
существует интеграл по сечению 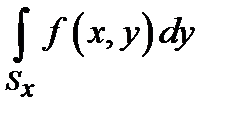 . В таком случае существует повторный интеграл
. В таком случае существует повторный интеграл 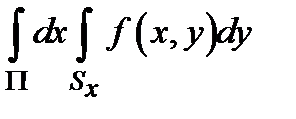 . При этом
. При этом 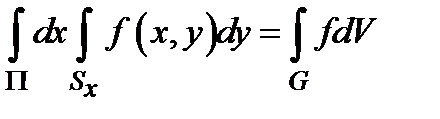 .
.
Отметим частные случаи, когда 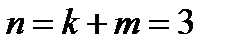 : 1)
: 1) 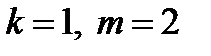 и 2)
и 2) 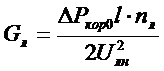 .
.
Замена переменных в кратных интегралах.
1˚.Перед тем как сформулировать правило замены переменных в кратных интегралах, напомним это правило в одномерном случае.
Рассмотрим гладкое отображение (замену переменной) 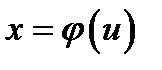 . Будем считать, что
. Будем считать, что 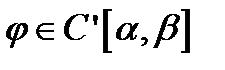 , причём
, причём 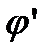 не обращается в нуль на отрезке
не обращается в нуль на отрезке 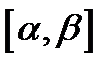 . Пусть еще
. Пусть еще 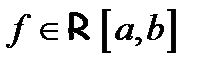 ,
, 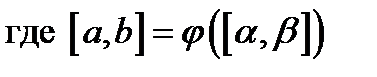 . Тогда
. Тогда 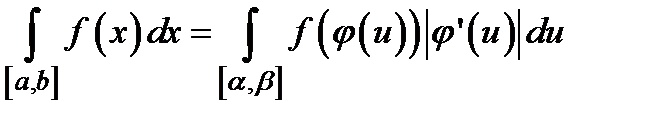 .
.
Теорема.Пусть 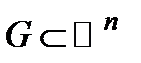 − область с кусочно-гладкой границей и
− область с кусочно-гладкой границей и 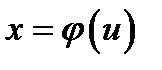 , где
, где 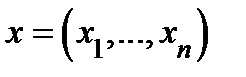 ,
, 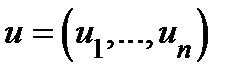 − взаимно однозначное отображение класса
− взаимно однозначное отображение класса 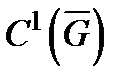 , причем якобиан этого отображения
, причем якобиан этого отображения 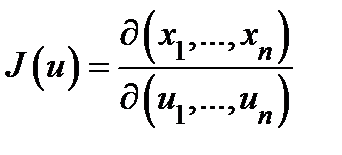 не обращается в нуль в области
не обращается в нуль в области 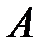 . Пусть ещё
. Пусть ещё 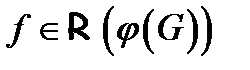 . Тогда
. Тогда
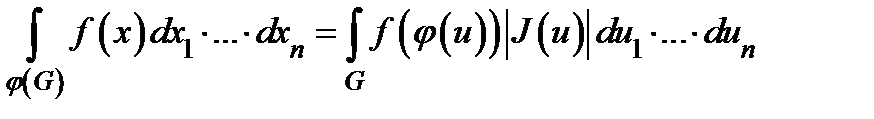 .
.
Эту формулу можно объяснить следующим образом. Из линейной алгебры известно, что 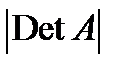 , где
, где 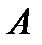 − линейный оператор
− линейный оператор 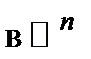 , показывает, во сколько раз изменяется объём любого параллелепипеда (и, значит, любого тела) под действием оператора
, показывает, во сколько раз изменяется объём любого параллелепипеда (и, значит, любого тела) под действием оператора 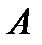 . Отсюда нетрудно вывести, что модуль определителя Якоби отображения
. Отсюда нетрудно вывести, что модуль определителя Якоби отображения 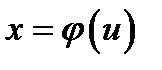 представляет собой коэффициент искажения объёма бесконечно малой окрестности точки под действием этого отображения.
представляет собой коэффициент искажения объёма бесконечно малой окрестности точки под действием этого отображения.
2˚. Криволинейные координаты в области 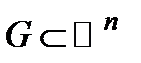 задаются с помощью гладкого взаимно однозначного отображения
задаются с помощью гладкого взаимно однозначного отображения 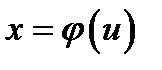 , для которого якобиан
, для которого якобиан 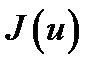 не обращается в нуль
не обращается в нуль 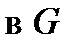 . Координатной линией
. Координатной линией 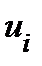
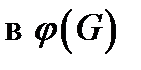 называются образ линии
называются образ линии 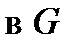 , вдоль которой изменяется только координата
, вдоль которой изменяется только координата 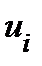 .
.
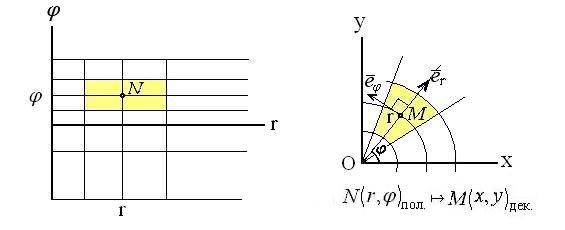
В качестве примера криволинейных координат рассмотрим полярные координаты на плоскости. В этом случае 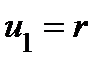 − полярный радиус точки
− полярный радиус точки 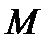 , отсчитываемый от полюса O,
, отсчитываемый от полюса O, 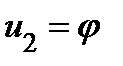 − полярный угол, отсчитываемый от полярной оси. Если
− полярный угол, отсчитываемый от полярной оси. Если 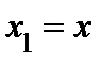 ,
, 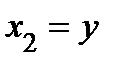 − координаты точки в правой прямоугольной декартовой системе координат, где ось
− координаты точки в правой прямоугольной декартовой системе координат, где ось 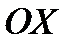 совпадает с полярной осью, то
совпадает с полярной осью, то 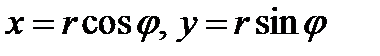 . Линии
. Линии 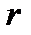 − лучи, выходящие из точки
− лучи, выходящие из точки  , линии
, линии 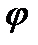 − окружности с центром в этой точке.
− окружности с центром в этой точке.
Вернёмся к общему случаю. По касательной к линии 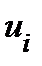 в заданной точке идёт вектор
в заданной точке идёт вектор 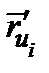 , который мы будем коротко записывать
, который мы будем коротко записывать 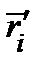 . Длина этого вектора называется
. Длина этого вектора называется 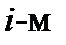 коэффициентом Ламэ и обозначается
коэффициентом Ламэ и обозначается 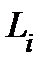 . По предыдущему
. По предыдущему 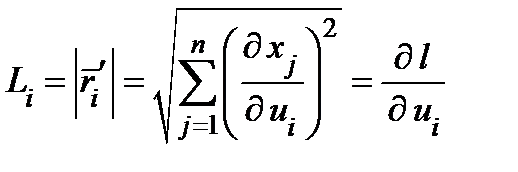 , т.е.
, т.е. 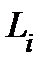 − коэффициент искажения длины вдоль линии
− коэффициент искажения длины вдоль линии 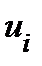 . В таком случае
. В таком случае 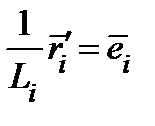 − единичный касательный вектор к линии
− единичный касательный вектор к линии 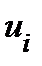 . Набор векторов
. Набор векторов 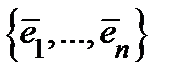 называется подвижным репером. Он, вообще говоря, зависит от точки, в которой вычислены все эти векторы. Если подвижный репер в каждой точке образует ортогональную систему векторов, то криволинейные координаты называются ортогональными.
называется подвижным репером. Он, вообще говоря, зависит от точки, в которой вычислены все эти векторы. Если подвижный репер в каждой точке образует ортогональную систему векторов, то криволинейные координаты называются ортогональными.
Имеем 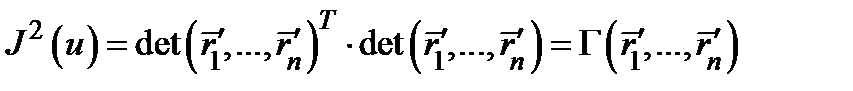 . В ортогональном случае из этой формулы, в частности, следует, что
. В ортогональном случае из этой формулы, в частности, следует, что
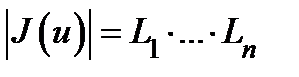 .
.
Таким образом, в случае перехода от прямоугольных декартовых координат к ортогональным криволинейным координатам коэффициент искажения объёма равен произведению коэффициентов искажения длины вдоль координатных направлений.
3˚. Важные примеры криволинейных координат.
1. Полярные координаты.Выше уже были описаны полярные координаты и их связь с прямоугольными декартовыми координатами. Коэффициенты Ламэ легко вычисляются, исходя из их геометрического смысла: 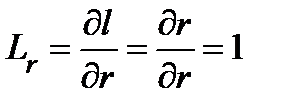 ,
, 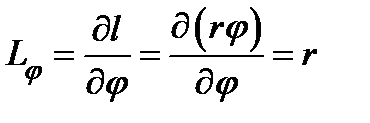 .
.
Подвижный репер состоит из взаимно ортогональных векторов 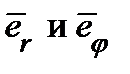 . Следовательно, полярные координаты представляют собой ортогональную криволинейную систему координат. Поэтому
. Следовательно, полярные координаты представляют собой ортогональную криволинейную систему координат. Поэтому 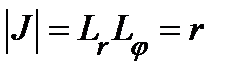 , иначе говоря,
, иначе говоря, 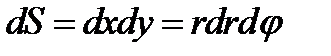 .
.
2. Обобщенные полярные (эллиптические) координаты. По определению они вводятся формулами 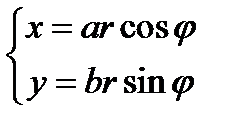 . Координатными линиями являются эллипсы
. Координатными линиями являются эллипсы 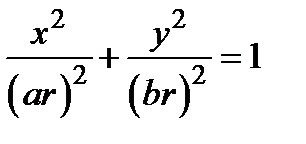 и лучи
и лучи 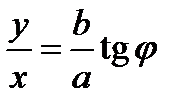 . Система − косоугольная. Здесь
. Система − косоугольная. Здесь 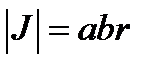 или
или 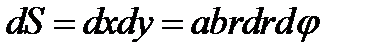 .
.
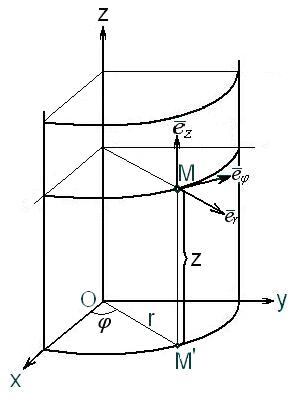
3. Цилиндрические координаты в пространстве.Так называются величины 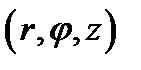 , где , где 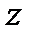 совпадает с соответствующей декартовой координатой совпадает с соответствующей декартовой координатой 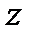 точки точки 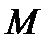 , а , а 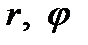 − полярные координаты точки − полярные координаты точки 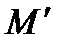 , являющейся проекцией , являющейся проекцией 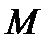 на плоскость на плоскость 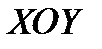 . Здесь . Здесь 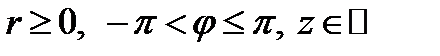 .
Линии .
Линии 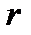 − лучи, расходящиеся от оси − лучи, расходящиеся от оси 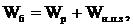 под прямым углом к ней. Линии под прямым углом к ней. Линии 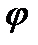 − окружности с центром на си − окружности с центром на си 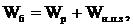 , лежащие в плоскостях , лежащие в плоскостях  . Линии . Линии 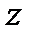 − прямые, параллельные оси − прямые, параллельные оси 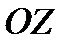 .
Координатные поверхности: полуплоскости .
Координатные поверхности: полуплоскости 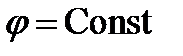 , начинающиеся с оси , начинающиеся с оси 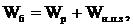 , плоскости , плоскости  , наконец, цилиндры , наконец, цилиндры  (давшие название системе).
Коэффициенты Ламэ: (давшие название системе).
Коэффициенты Ламэ: 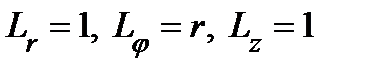 . Данная система является ортогональной. . Данная система является ортогональной.
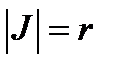 , т.е. , т.е. 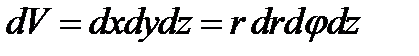 . .
| 
|
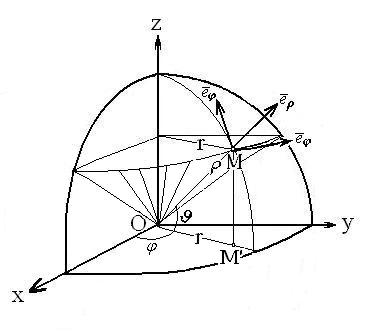
4. Сферические координаты в пространстве.Так называются величины 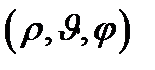 , где , где 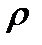 − расстояние точки − расстояние точки 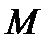 от начала координат; от начала координат; 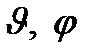 − широта и долгота точки; − широта и долгота точки; 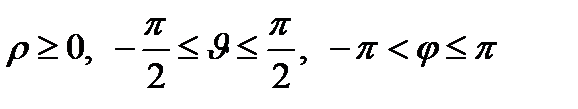 . При этом . При этом 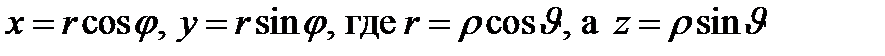 , или , или
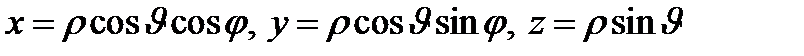 .
Линии .
Линии 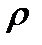 − лучи, выходящие из начала координат; линии − лучи, выходящие из начала координат; линии 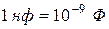 − меридианы; линии − меридианы; линии 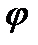 − параллели. Координатные поверхности – сферы − параллели. Координатные поверхности – сферы 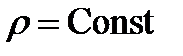 , конусы , конусы  и полуплоскости и полуплоскости 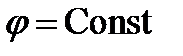 , начинающиеся с оси , начинающиеся с оси 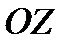 .
Коэффициенты Ламэ: .
Коэффициенты Ламэ: 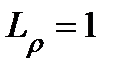 , , 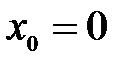 , , 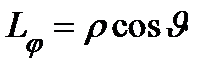 .
Так как сферическая система является ортогональной, то .
Так как сферическая система является ортогональной, то
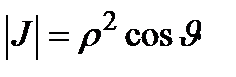 , , 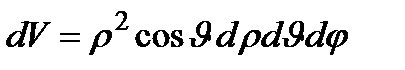 . .
|
|
Приложения кратных интегралов.
1˚. Геометрические приложения.
Конечно, для полного рассмотрения вопроса 'Замена переменных в кратных интегралах.', приведенной информации не достаточно, однако чтобы понять основы, её должно хватить. Если вы изучаете эту тему, с целью выполнения задания заданного преподавателем, вы можете обратится за консультацией в нашу компанию. В нашей команде работает большой состав специалистов, которые разбираются в изучаемом вами вопросе на экспертном уровне.


 .
.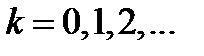 с помощью плоскостей
с помощью плоскостей 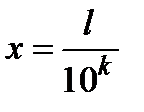 ,
, 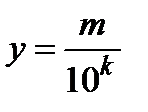 ,
, 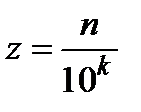 ,
, 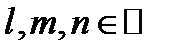 . Обозначим
. Обозначим 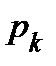 количество кубов
количество кубов 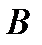 и
и 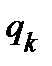 − количество кубов
− количество кубов 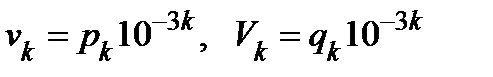 .
.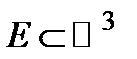 называется величина
называется величина 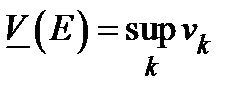 . Внешней мерой Жордана множества
. Внешней мерой Жордана множества 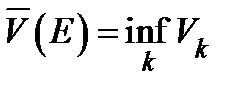 . Множество
. Множество 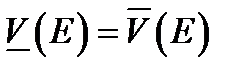 . Их общее значение
. Их общее значение 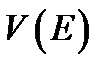 называется просто мерой этого множества или его объёмом.
называется просто мерой этого множества или его объёмом.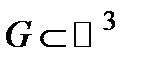 − кубируемое, ограниченное множество и
− кубируемое, ограниченное множество и 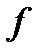 − функция, определенная на этом множестве. Рассмотрим разбиение
− функция, определенная на этом множестве. Рассмотрим разбиение 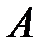 на неперекрывающиеся кубируемые подмножества
на неперекрывающиеся кубируемые подмножества 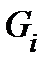 и выберем точки
и выберем точки 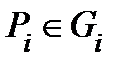 . Обозначим
. Обозначим 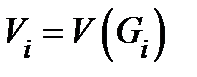 − объём множества
− объём множества 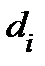 диаметр этого множества. Назовем мелкостью разбиения
диаметр этого множества. Назовем мелкостью разбиения 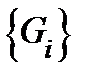 величину
величину 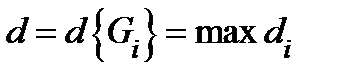 . Образуем интегральную сумму Римана
. Образуем интегральную сумму Римана 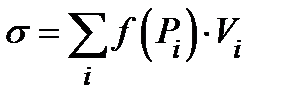 .
.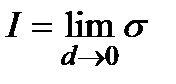 , то функция
, то функция 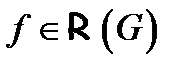 , а сам предел называется тройным интегралом и обозначается
, а сам предел называется тройным интегралом и обозначается 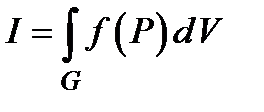 или
или 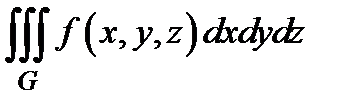 .
.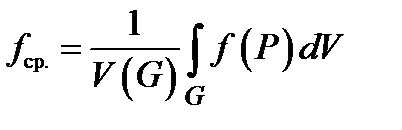 .
. при любом натуральном
при любом натуральном 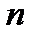 .
.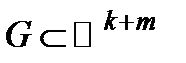 ,
, 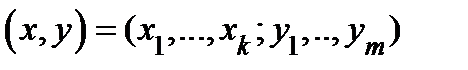 ;
; 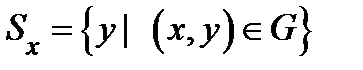 − сечение множества
− сечение множества  и пусть
и пусть 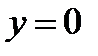 (т.е. на подпространство первых координат).
(т.е. на подпространство первых координат).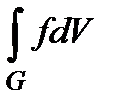 и пусть при любом значении
и пусть при любом значении 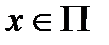 существует интеграл по сечению
существует интеграл по сечению 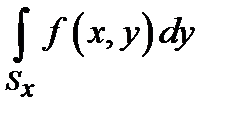 . В таком случае существует повторный интеграл
. В таком случае существует повторный интеграл 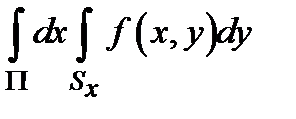 . При этом
. При этом 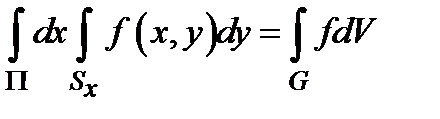 .
.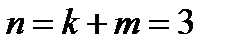 : 1)
: 1) 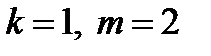 и 2)
и 2) 
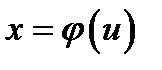 . Будем считать, что
. Будем считать, что 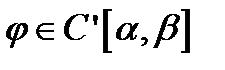 , причём
, причём 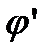 не обращается в нуль на отрезке
не обращается в нуль на отрезке 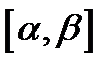 . Пусть еще
. Пусть еще 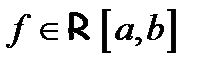 ,
, 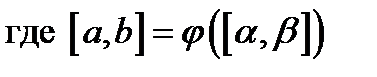 . Тогда
. Тогда 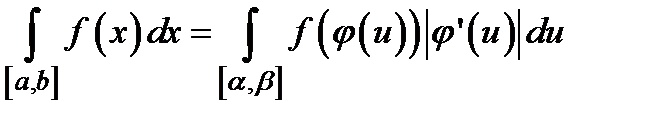 .
.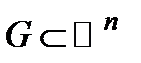 − область с кусочно-гладкой границей и
− область с кусочно-гладкой границей и 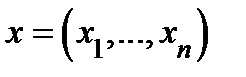 ,
, 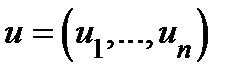 − взаимно однозначное отображение класса
− взаимно однозначное отображение класса 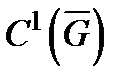 , причем якобиан этого отображения
, причем якобиан этого отображения 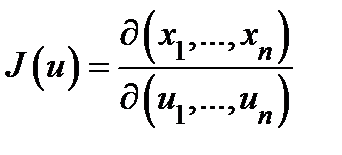 не обращается в нуль в области
не обращается в нуль в области 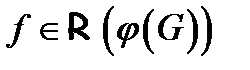 . Тогда
. Тогда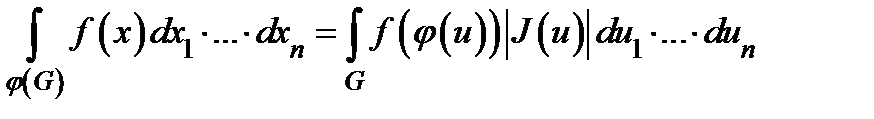 .
.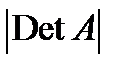 , где
, где 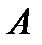 − линейный оператор
− линейный оператор 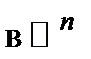 , показывает, во сколько раз изменяется объём любого параллелепипеда (и, значит, любого тела) под действием оператора
, показывает, во сколько раз изменяется объём любого параллелепипеда (и, значит, любого тела) под действием оператора 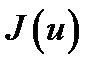 не обращается в нуль
не обращается в нуль 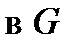 . Координатной линией
. Координатной линией 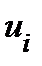
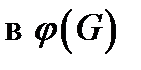 называются образ линии
называются образ линии 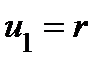 − полярный радиус точки
− полярный радиус точки 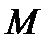 , отсчитываемый от полюса O,
, отсчитываемый от полюса O, 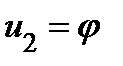 − полярный угол, отсчитываемый от полярной оси. Если
− полярный угол, отсчитываемый от полярной оси. Если 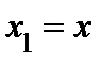 ,
, 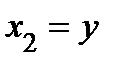 − координаты точки в правой прямоугольной декартовой системе координат, где ось
− координаты точки в правой прямоугольной декартовой системе координат, где ось 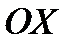 совпадает с полярной осью, то
совпадает с полярной осью, то 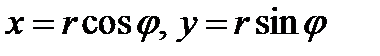 . Линии
. Линии 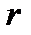 − лучи, выходящие из точки
− лучи, выходящие из точки  , линии
, линии 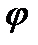 − окружности с центром в этой точке.
− окружности с центром в этой точке.
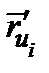 , который мы будем коротко записывать
, который мы будем коротко записывать 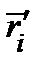 . Длина этого вектора называется
. Длина этого вектора называется 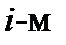 коэффициентом Ламэ и обозначается
коэффициентом Ламэ и обозначается 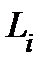 . По предыдущему
. По предыдущему 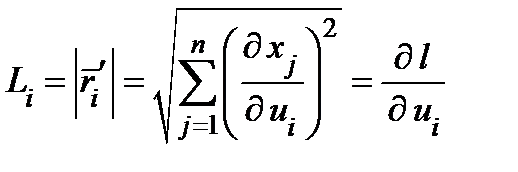 , т.е.
, т.е. 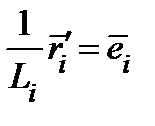 − единичный касательный вектор к линии
− единичный касательный вектор к линии 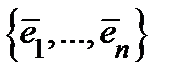 называется подвижным репером. Он, вообще говоря, зависит от точки, в которой вычислены все эти векторы. Если подвижный репер в каждой точке образует ортогональную систему векторов, то криволинейные координаты называются ортогональными.
называется подвижным репером. Он, вообще говоря, зависит от точки, в которой вычислены все эти векторы. Если подвижный репер в каждой точке образует ортогональную систему векторов, то криволинейные координаты называются ортогональными.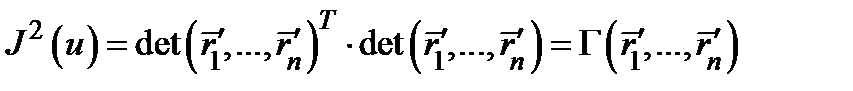 . В ортогональном случае из этой формулы, в частности, следует, что
. В ортогональном случае из этой формулы, в частности, следует, что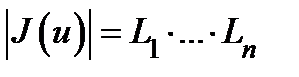 .
.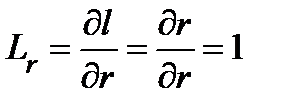 ,
, 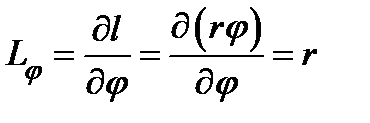 .
.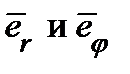 . Следовательно, полярные координаты представляют собой ортогональную криволинейную систему координат. Поэтому
. Следовательно, полярные координаты представляют собой ортогональную криволинейную систему координат. Поэтому 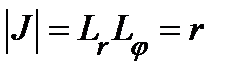 , иначе говоря,
, иначе говоря, 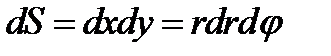 .
.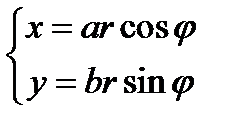 . Координатными линиями являются эллипсы
. Координатными линиями являются эллипсы 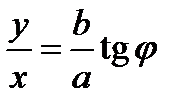 . Система − косоугольная. Здесь
. Система − косоугольная. Здесь 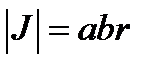 или
или 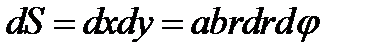 .
.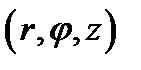 , где
, где 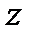 совпадает с соответствующей декартовой координатой
совпадает с соответствующей декартовой координатой 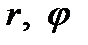 − полярные координаты точки
− полярные координаты точки 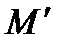 , являющейся проекцией
, являющейся проекцией 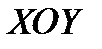 . Здесь
. Здесь 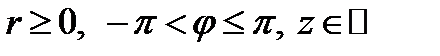 .
Линии
.
Линии  . Линии
. Линии 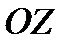 .
Координатные поверхности: полуплоскости
.
Координатные поверхности: полуплоскости 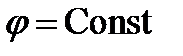 , начинающиеся с оси
, начинающиеся с оси 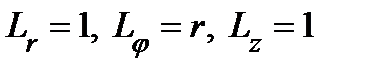 . Данная система является ортогональной.
. Данная система является ортогональной.
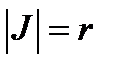 , т.е.
, т.е. 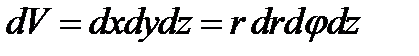 .
.

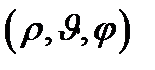 , где
, где 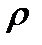 − расстояние точки
− расстояние точки 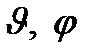 − широта и долгота точки;
− широта и долгота точки; 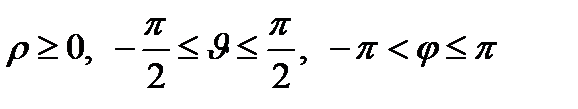 . При этом
. При этом 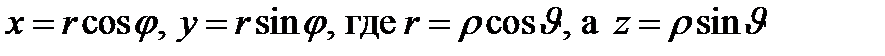 , или
, или
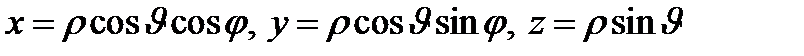 .
Линии
.
Линии 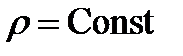 , конусы
, конусы  и полуплоскости
и полуплоскости 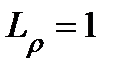 ,
, 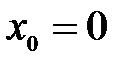 ,
, 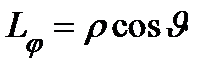 .
Так как сферическая система является ортогональной, то
.
Так как сферическая система является ортогональной, то
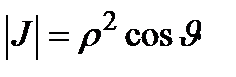 ,
, 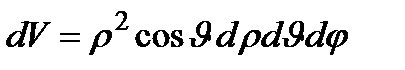 .
.






